Toets Natuurkunde
Nova Natuurkunde 4e ed - Hoofdstuk 1 - Krachten oefentoetsen & antwoorden
4e editie
Deze toets behandelt de volgende onderwerpen: Vervorming, Soorten krachten, krachten tekenen, Zwaartepunt, Evenwicht, Uitrekking, Normaalkracht, Samengestelde krachten, Krachten in het heelal, Gewicht, Hefbomen, Moment, Momentenwet, Katrollen, Arbeid, Druk, Soorten evenwicht, Middelpuntzoekende kracht en Hydraulische werktuigen.
Toets Natuurkunde
Nova Natuurkunde 4e ed
- a) Bij plastische vervorming.
- Toelichting: Je hebt plastische en elastische vervorming. Bij elastische vervorming is een vervorming niet blijvend nadat er op een materiaal kracht uitgeoefend is. Bij plastische vervorming is dit wel blijvend.
- b) Rolwrijving en luchtwrijving zijn de wrijvingskrachten die een tegenwerkende kracht kunnen veroorzaken.
- c) De stugheid van een veer geeft aan hoe makkelijk die uitrekt. Hoe stugger een veer hoe lastiger deze dan uitrekt. Hoe stugger de veer, hoe meer kracht je nodig hebt om de veer uit te rekken. Een hele stugge veer heeft dus ook een grote veerconstante.
- d) De middelpuntzoekende kracht.
- e) Gewicht en de zwaartekracht zijn niet hetzelfde. Het gewicht van een voorwerp is een gevolg van de zwaartekracht. Bijvoorbeeld: Een pak suiker met een massa van 1 kilogram wordt hier op aarde met 9,81 N/kg aangetrokken door de zwaartekracht. Dit betekent dat het gewicht van het pak suiker op aarde Fz = m * g = 1,0 * 9,8 = 9,8 N is. Het pak suiker oefent dus een kracht van 9,81 N uit op zijn ondergrond. Zouden we ditzelfde pak suiker op Mars op een tafel neerzetten is het gewicht anders. Op Mars wordt er aan hetzelfde pak suiker met een kracht van 3,74 N/kg getrokken (de zwaartekracht is daar dus minder sterk). Dit betekent dat het pak suiker daar een gewicht heeft van
- Fz = m * g = 1,0 * 3,74 = 3,74 N .
- De massa is dus overal hetzelfde. Dit geldt niet dus niet voor gewicht.
- f) Bij iedere hefboom beweegt het object rondom een draaipunt. Het moment geeft aan hoe sterk een voorwerp kan draaien.
- g) Een takel wordt gebruikt om objecten met grote massa’s met minder kracht dan de zwaartekracht van dat object te verplaatsen.
- Voorbeeld van een goede tekening:
-
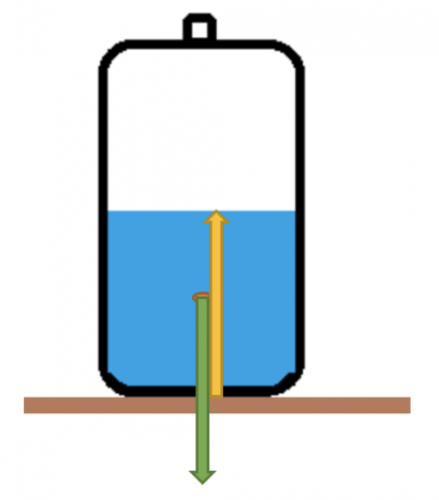
- Er werken twee krachten op het flesje: de zwaartekracht (omlaag gericht) en de normaalkracht die de tafel op het flesje uitoefent (omhoog gericht).
- Zwaartekracht (groene pijl):
- De zwaartekracht die op het flesje werkt is Fz = m * g = 0,26 kg * 9,8 = 2,55 N . Het gewicht van het flesje is dus 2,55 N en dit wordt uitgeoefend op het tafelvlak. Deze zwaartekracht werkt vanuit het zwaartepunt (oranje stip) van de bidon.
- De bidon van 500 ml is voor de helft gevuld met water, dit is dus 250 ml. Dat betekent dat de bidon zelf een massa heeft van 260 - 250 = 10 gram. Het zwaartepunt van de half gevulde bidon zal in het midden van het water te vinden zijn (de massa van het water is namelijk aanzienlijk groter in verhouding tot enkel de bidon van 10 gram).
- De tekenschaal is 1 cm = 1 N , dit betekent dat je vanuit het zwaartepunt een pijl van 2,55N / 1cm/N = 2,55 centimeter recht omlaag tekent.
- Normaalkracht (gele pijl):
- De normaalkracht is de kracht die de tafel uitoefent op de bidon. Als deze kracht er niet zou zijn, zou de bidon door de tafel heen gaan. De twee krachten in deze situatie heffen elkaar op, het geheel is dus in balans. Dit betekent dat de normaalkracht precies even groot is als de zwaartekracht die op de bidon werkt.
- De normaalkracht teken je vanaf het contactpunt tussen de tafel en de bidon dus ook met een lengte van 2,55 centimeter recht omhoog.
- De zwaartekracht op de piano, de spierkracht van de man en de spankracht in de touwen spelen hierbij een rol.
- Een satelliet wordt aangetrokken door de aarde. De zwaartekracht werkt hier dus nog (heel zwakjes) op. Hierdoor is de satelliet continu in een vrije val. Doordat de satelliet een hoge baansnelheid heeft komt deze nooit op aarde terecht. De satelliet blijft namelijk om de aarde heen draaien. Het is daardoor continu in een vrije val. Voorwerpen die constant in een vrije val verkeren, zijn in feite gewichtloos.
- De piano hangt aan drie touwen van een takel. Dit betekent dat de benodigde spierkracht drie maal zo klein zal zijn als de zwaartekracht die werkt op de piano en dat de hoeveelheid touw drie maal zoveel zal zijn als de zes meter.
- De benodigde hoeveelheid touw is dus 6 * 3 = 18 meter.
- Met Fz = m * g valt de zwaartekracht die werkt op de piano te bereken. Invullen geeft: Fz = m * g = 450 * 9,8 = 4410 N
- Dankzij de takel zal de benodigde spierkracht drie maal zo klein zijn als de 4410 N. Dit geeft 4410/3 = 1470 N
- De arbeid kan berekend worden met de formule W = F * s , invullen geeft:
- W = 1470 N * 18 m = 26460 J
- Let op: Dit is hetzelfde antwoord dat je krijgt wanneer je met de basisgegevens uit de vraag de formule voor arbeid in zou vullen, namelijk: 4410 N * 6 m = 26460 J . Echter, is de vraag dan niet volledig beantwoord. Er wordt specifiek gevraagd om met de benodigde spierkracht en de hoeveelheid touw die binnengehaald moet worden de arbeid te berekenen.
- Ten slotte moet je de groene pijl meten (dit is namelijk de nettokracht). De pijl is ongeveer 5,9 centimeter lang. Berekenen met de krachtenschaal geeft dan 30 N/cm * 5,9 = 177 N . De nettokracht is dus 177 N.
- Meestal wordt bij opgaven waar je zelf zaken moet opmeten rekening gehouden met een onnauwkeurigheid van maximaal 10%.
- Gegevens:
- Massa B = 90 kg
- Afstand B tot draaipunt = 2 m
- De wip is 6 meter lang en het draaipunt zit precies op de helft van de wip. Dit is dus op 3 meter. Persoon A zit op het uiteinde en dus is de afstand tot het draaipunt 3 meter.
- Gevraagd: Massa A
- Formules:
- Zwaartekracht
- Fz = m * g
- Momentenwet
- FA * rA = FB * rB
- Ma = Mb
- Invullen:
- FzB = m * g = 90 * 9,8 = 882 N
- FA * rA = FB * rB
- Invullen geeft: Fa * 3 m = 882 N * 2 m = 1764 Nm
- Het moment voor FA * rA is even groot. Dit komt doordat de wip in evenwicht is.
- FA * rA = M invullen geeft FA * 3 m = 1764 Nm
- → FA = 1764Nm / 3 m = 588 N
- Dit is dus de zwaartekracht die werkt op persoon A.
- FzA = m * g = m * 9,8 N/kg = 588 N
- → m = 588/9,8 = 60 kg
- Persoon A heeft dus een massa van 60 kilogram.
- Deze vraag bestaat uit twee delen: eerst de kracht die de onbekende stof op de veer uitoefent berekenen en vervolgens met dat gegeven de massa van de onbekende stof berekenen.
- De kracht die op de veer wordt uitgeoefend kan berekend worden met F = C * u . Dit invullen geeft: F = 2 N/cm * 11,5 cm = 23 N . Dit is de kracht die op de veer wordt uitgeoefend wanneer de onbekende stof aan de veer hangt. Dit is ook de zwaartekracht die werkt op de onbekende stof. Daarmee valt verder te rekenen.
- Vervolgens kan met de formule Fz = m * g berekend worden wat de massa van de onbekende stof is.
- Invullen geeft: Fz = m * g → m = Fz/g = 23N /1,62N/kg = 14,198 kg
- In deze situatie zijn er twee voorwerpen. Bij simpel gevormde voorwerpen kan er gesteld worden dat de zwaartepunten uit het midden van de voorwerpen werken. Ieder deel van de balk is 0,5 meter. Halverwege de balk, dus op 1,25 meter, ligt het zwaartepunt van de balk. Dit ligt 1,5 - 1,25 = 0,25 meter links van het draaipunt. De steen heeft een zwaartepunt dat op een afstand van 0,5 meter werkt rechts van het draaipunt.
- De zwaartekracht die werkt op de steen is Fz = m * g = 1,5 * 9,8 = 14,7 N .
- De massa van de balk wordt gevraagd.
- De balk is in balans, dat betekent dat de momentenwet toegepast mag worden: M = Fl * rl = Fr * rr , invullen geeft:
- Fl * 0,25 m = 14,7 N * 0,5 m = 7,35 Nm
- Fl = M/Fr = 7,35 Nm / 0,25 m = 29,4 N
- Massa met Fz = m * g berekenen geeft
- → m = Fz/g = 29,4N / 9,8 N.kg = 3 kg
- De massa van de balk is dus 3 kg.
- De zwaartekracht op de bowlingbal is Fz = m * g = 6kg * 9,8N/kg = 58,8 N .
- Door het gebruik van de helling is de benodigde spierkracht 8,4m/1,2m = 7 maal zo klein om de bowlingbal bovenaan de helling te krijgen, maar is de afstand dus wel 7 maal zo groot ten opzichte van de hoogte van 1,2 meter.
- De benodigde spierkracht is dus 7 maal zo klein als de zwaartekracht die werkt op de bowlingbal en dat is dus 58,8 N / 7 = 8,4 N %
- W = F * s invullen geeft:
- W = 8,4N * 8,4m = 70,56 J
- Let op: Dit is hetzelfde antwoord dat je krijgt wanneer je met de basisgegevens uit de vraag de formule voor arbeid in zou vullen, namelijk: 58,8N * 1,2 m = 70,56 J . Echter, is de vraag dan niet volledig beantwoord. Er wordt specifiek gevraagd om met de benodigde spierkracht en de hoeveelheid touw die binnengehaald moet worden de arbeid te berekenen.
Deze toets bestellen?
Voordeligst
Lidmaatschap ToetsMij
€ 12,99/mnd
- Snel nog even wat toetsen oefenen? Kies dan onze meest flexibele optie.
- Je kunt maandelijks opzeggen.
- Toegang tot alle vakken bij ToetsMij.
Wat krijg je bij een abonnement?
- Toegang tot alle vakken
- 20 kwalitatieve oefentoetsen per maand
- Antwoorden, uitwerkingen en toelichtingen
- Geen stress voor het maken van toetsen
Eenvoudig en veilig betalen met iDEAL of creditcard
3 maanden ToetsMij
€ 12,99
€ 10,99/mnd
- Voordelig en flexibel. Ideaal als je maar een paar maanden toetsen hoeft te gebruiken.
- Betaal per kwartaal en bespaar hiermee 2 euro per maand.
- Toegang tot alle vakken bij ToetsMij.
Wat krijg je bij een abonnement?
- Toegang tot alle vakken
- 20 kwalitatieve oefentoetsen per maand
- Antwoorden, uitwerkingen en toelichtingen
- Geen stress voor het maken van toetsen
Eenvoudig en veilig betalen met iDEAL of creditcard
1 jaar ToetsMij
€ 12,99
€ 7,50/mnd
- Favoriete keuze van meer dan 70% van de gebruikers.
- Betaal slechts 90 euro per jaar en bespaar hiermee 65 euro.
- Geniet van een volledig jaar toegang tot alle vakken bij ToetsMij.
Wat krijg je bij een abonnement?
- Toegang tot alle vakken
- 20 kwalitatieve oefentoetsen per maand
- Antwoorden, uitwerkingen en toelichtingen
- Geen stress voor het maken van toetsen
Eenvoudig en veilig betalen met iDEAL of creditcard
Waarom ToetsMij?
- Betere schoolresultaten
- Geen stress meer omdat je weet wat je moet doen om je toetsen te halen
- Direct toegang tot antwoorden en uitwerkingen zodat je weet wanneer je klaar bent voor je toets
Heb je nog vragen?
Neem eenvoudig contact met ons op, of kijk bij onze veelgestelde vragen.
Dit zeggen leerlingen en ouders
Cijfers omhoog
Onze zoon had in februari zeker 12 minpunten. Hij is gestart met oefenen via Toets mij en heeft een geweldige eindsprint getrokken en afgelopen week bijna het onmogelijke waargemaakt. Er zijn nog maar 2 minpunten over en nog niet alle toetsen zijn terug. Het heeft onze zoon enorm geholpen, omdat er breed getoetst wordt en de vraagstelling, zoals van hem begrepen, overeenkomt met de toets. Als je de oefentoetsen goed kunt maken, beheers je de stof echt goed!
AP
Fijn dat leerlingen alvast een keer een toets kunnen oefenen die eruit ziet zoals op school.
Wij hebben sinds kort Toetsmij, omdat onze dochter het erg lastig heeft met Wiskunde. Op deze manier kan ze het hoofdstuk oefenen met een toets die qua vraagstelling overeenkomt met de toetsen op school. Nu kan ze dit dus eerst oefenen voordat ze de echte toets moet doen. Als docent Engels die werkt met Of Course en All Right kan ik bevestigen dat de toetsen grotendeels overeenkomen met de vraagwijze van de methode zelf. Dat is dus heel fijn voor leerlingen om te oefenen. We hadden heel even een dingetje met het nakijken, want de uitwerkingen werden niet goed weergegeven. Even een mailtje en binnen een dag reactie en ICT ging meteen aan de slag met het herstellen van de uitwerkingen. Super contact, goede dienstverlening! Aanrader!
Lelani van den Berg
Zéér tevreden!!
Lid geworden voor mijn zoon in leerjaar 1 van (toen 13) inmiddels 15. Hij zit nu in leerjaar 3 HAVO. Elk boek is makkelijk te vinden en alsmede mailt met een probleem omdat hij Duits krijgt uit een boek van leerjaar 2 word dit zelfs op zondag binnen een half uur opgelost en toegevoegd aan ons account! Zo’n toffe service zie je niet vaak meer! Dus wij zijn zéér tevreden. Sinds we het nu weer gebruiken (tijdje niet gebruikt) scoort hij weer voldoendes en zelf voor wiskunde een 8.8!
Linda Ockers
Zoek in meer dan 10.000 toetsen
Echte toetsvragen, precies aansluitend op jouw lesmethode en leerjaar. Voor klas 1 t/m 6 van vmbo-t t/m gymnasium.
