Toets Natuurkunde
Nova Natuurkunde 4e ed - Hoofdstuk 1 - Krachten oefentoetsen & antwoorden
4e editie
Deze toets behandelt de volgende onderwerpen: Vervorming, Soorten krachten, krachten tekenen, Zwaartepunt, Evenwicht, Uitrekking, Normaalkracht, Samengestelde krachten, Krachten in het heelal, Gewicht, Hefbomen, Moment, Momentenwet, Katrollen, Arbeid, Druk, Soorten evenwicht, Middelpuntzoekende kracht en Hydraulische werktuigen.
Toets Natuurkunde
Nova Natuurkunde 4e ed
- a) Bij elastische vervorming.
- Toelichting: Je hebt plastische en elastische vervorming. Bij elastische vervorming is een vervorming niet blijvend nadat er op een materiaal kracht uitgeoefend is. Bij plastische vervorming is dit wel blijvend.
- b) Een krachtenschaal gebruik je om met in tekeningen de grootte en richting van een kracht aan te geven. Door de lengte van een pijl in een getekende situatie met krachten te meten, kan je achter de krachtenschaal in een situatie komen. Dit geeft dan aan hoeveel Newton één centimeter is.
- c) Druk geeft aan hoeveel kracht er op één vierkante meter wordt uitgeoefend. Dit kan je bereken met de formule p = F/A, waarbij je dus de kracht die op een oppervlak wordt uitgeoefend deelt door de grootte van het oppervlak.
- d) De veerconstante geeft aan hoeveel kracht er op een veer uitgeoefend moet worden om deze één centimeter uit te rekken. Er geldt hoe groter de veerconstante van een veer is, hoe stugger de veer.
- e) Massa en gewicht is niet hetzelfde. Massa geeft een hoeveelheid stof aan en we gebruiken daar vaak de eenheid gram of kilogram voor. Gewicht is een gevolg van de zwaartekracht die werkt op een massa. Het geeft aan hoeveel kracht de massa uitoefent wanneer het ergens op staat of aan hangt. Hoe groter de zwaartekracht die werkt op een massa, hoe groter het gewicht van de massa dus is. De massa van 1 kg bananen is bijvoorbeeld op de aarde en de maan hetzelfde, maar het gewicht niet. Dit komt doordat de zwaartekracht op aarde groter is dan de zwaartekracht op de maan.
- f) Arbeid geeft aan hoeveel een krachtbron zich in moet spannen om een massa te verplaatsen.
- g) Door een hefboom te gebruiken kan je minder spierkracht nodig hebben om een grote kracht ergens op uit te oefenen. Bijvoorbeeld bij een moersleutel, deze gebruik je als een hefboom. Door de hefboomwerking is de kracht die je uitoefent op een moer groter dan de daadwerkelijke spierkracht.
- a) De drie kenmerken van een vectorgrootheid zijn:
- Een grootte (in een tekening aangegeven met de lengte van de pijl)
- Een richting
- Een aangrijpingspunt (in een tekening het startpunt van de pijl)
- b) Voorbeeld van een goede tekening (met krachtenschaal 1 cm = 100 N)
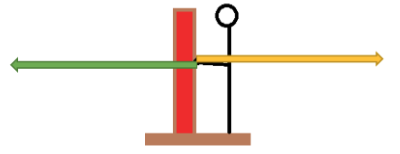
- Er werken twee krachten tussen de man en de muur: de spierkracht van de man (naar links gericht) en de normaalkracht die de muur tegenovergesteld aan de spierkracht van de man uitoefent (naar rechts gericht).
- Spierkracht (groene pijl):
- De spierkracht die de man uitoefent is 450 N. De tekenschaal is 1 cm = 100 N. Dit betekent dat de pijl 450/100 = 4,5 cm lang moet zijn.
- De pijl start vanaf het punt waar de man contact heeft met de muur. Dit is het aangrijpingspunt.
- De man duwt tegen de muur aan, dus de richting van de kracht is naar links gericht.
- Normaalkracht (gele pijl):
- De normaalkracht is de kracht die de muur uitoefent tegengesteld aan de spierkracht van de man. Anders zou er geen sprake zijn van een krachtenevenwicht.
- De normaalkracht is heeft dezelfde grootte als de spierkracht. Dit betekent dat de pijl die getekend moet worden ook 4,5 cm lang is.
- De pijl start ook op het punt waar er contact is tussen de muur en de man.
- De normaalkracht heft de spierkracht precies op. Dit betekent dat de richting exact tegenovergesteld is aan de spierkracht van de man en dus naar rechts is gericht.
- Let op: In deze uitwerking is er gewerkt met een krachtenschaal van 1 cm = 100 N. Bij een ander gekozen krachtenschaal zijn de lengtes van de pijlen anders. Bijvoorbeeld bij een schaal 1 cm = 50 N zouden de pijlen 450/50 = 9 cm per stuk zijn.
- c) De muur zou instabiel in evenwicht zijn wanneer het zwaartepunt van de muur boven het steunvlak komt. Dan zou deze omvallen.
- De spierkracht die de man uitoefent op de speelt een rol. Verder speelt de spankracht in de boog een rol. Wanneer de man de gespannen boog loslaat, zal door de spankracht de pijl worden weggeschoten.
- Wanneer we kijken naar de formule Fmpz = m * v2/r, dan is de straal de noemer in deze breuk. Dit betekent dat hoe groter de straal is, hoe kleiner de middelpuntzoekende kracht zal zijn. Dit klopt volgens de theorie ook. Voor een draaiend voorwerp met een kleine baan is een grotere middelpuntzoekende kracht nodig dan voor hetzelfde voorwerp met een grotere baan ergens omheen.
- Doordat er een tweede massa aan de kant van persoon A is gaan zitten, is het moment aan die zijde groter geworden. Wanneer het moment aan beide kanten van de wipwap even groot is, is de wipwap in evenwicht. Persoon B kan aan de eigen zijde het moment groter maken door op meer afstand van het draaipunt te gaan zitten, want M = F * r. Persoon B kan zijn massa niet veranderen en daarmee dus ook niet de kracht die persoon B uitoefent op de wipwap. Meer afstand nemen van het draaipunt is dus de enige mogelijkheid om de wipwap weer in evenwicht te krijgen.
- Wanneer zuiger A in wordt gedrukt, levert dit een bepaalde druk. Dit kan je bereken met p = F/A. Die druk wordt op de vloeistof geleverd en daardoor uiteindelijk ook uitgeoefend op zuiger B.
- Zuiger B heeft een groter oppervlak. Dezelfde druk die A leverde op de vloeistof, komt nu op zuiger B terecht. Dat betekent dat de druk (p) gelijk blijft, terwijl dit wel op een groter oppervlak wordt uitgeoefend. Als we weer kijken naar de formule voor druk p = F/A zien we dat dit wel moet betekenen dat de kracht die op zuiger B in totaal uitgeoefend wordt, groter is. Wanneer dit niet het geval zou zijn, zou de druk niet dezelfde waarde kunnen behouden.
- Er geldt een krachtenschaal van 1 cm = 100 N. Eerst de grootte van de krachten berekenen:
- De pijl omhoog gericht is 5 cm. De kracht omhoog is dus 5 * 100 = 500 N groot.
- De pijl naar rechts gericht is 3,5 cm. De kracht naar rechts is dus 3,5 * 100 = 350 N groot.
- Met de stelling van pythagoras kan de resultante kracht berekend worden. Dit kan omdat de hoek tussen de twee krachten 90° is. Berekenen geeft:
- Gegevens:
- $F_{omhoog} = 500N$
- $F_{rechts} = 350 N$
- Gevraagd: Resultante kracht $F_{res}$
- Formule: $F_{res}^2 = F_{omhoog}^2 + F_{rechts}^2$
- Vervolgens voor de resultante kracht de wortel trekken van bovenstaande optelsom.
- Invullen: $F_{res}^2 = F_{omhoog}^2 + F_{rechts}^2$ = 500² + 350² = 372500
- √372500 = 610,33 N
- De resultante kracht die op de paal werkt is dus 610,33 N.
- Het gaat om een takel met vier touwen. Dit betekent dat op de veer maar een kwart (1/4de) van de totale zwaartekracht van de boekenkast werkt.
- De veer rekt 1,47 meter uit en heeft een veerconstante van 100 N/m. Invullen geeft: F = C * u = 100 N/m * 1,47 m = 147 N. Op de veer werkt dus een kracht van 147N.
- De zwaartekracht die werkt op de boekenkast en die vervolgens dus spankracht veroorzaakt in de touwen van de kabel, verdeeld zich evenredig over de vier touwen. Dit betekent dat de totale zwaartekracht vier maal zo groot is als de kracht die op de veer werkt. Dit is dan dus in totaal 147 N * 4 = 588 N. De totale zwaartekracht op de boekenkast is dus 588 N.
- Met de formule Fz = m * g kan je nu de massa berekenen van de boekenkast. De formule toepassen geeft dan m = Fz/g = 588/9,8= 60 kg.
- De boekenkast heeft dus een massa van 60 kilogram.
- De veer wordt weer vervangen door een normaal touw. Vervolgens worden er nog eens vier touwen aan de takel toegevoegd. Hierdoor heeft de takel nu acht touwen.
- b)
- 1.
- Antwoord: Dit is onjuist.
- Toelichting: De arbeid die geleverd moet worden blijft hetzelfde. Wanneer we kijken naar de formule W = F * s betekent dit namelijk dat er meer touw (afstand) binnen gehaald moet worden. Hiervoor is wel minder spierkracht nodig. Maar de benodigde arbeid blijft in alle gevallen gelijk.
- 2.
- Antwoord: Dit is onjuist.
- Toelichting: Door de hoeveelheid touw te verdubbelen, moet er juist ook tweemaal zoveel touw binnengehaald worden.
- 3.
- Antwoord: Dit is juist.
- Toelichting: Door de hoeveelheid touw te verdubbelen, wordt de totale zwaartekracht die werkt op de boekenkast over tweemaal zo veel touwen verdeeld. Hierdoor is de benodigde spierkracht om de boekenkast te verplaatsen gehalveerd.
- Inzicht krijgen in de situatie: Kijk eerst naar hoe de situatie in elkaar zit en wat er nu eigenlijk van je gevraagd wordt. Een paar belangrijke zaken zijn dan:
- Het draaipunt in deze situatie ligt op het rechter uiteinde van de kist waar de plank op kan kantelen. Zie de rode stip in het plaatje.
- De afstand tussen dit draaipunt (rode stip) en het zwaartepunt van de plank bedraagt 0,6 meter.
- De vraag herformuleren: Hoeveel centimeter moet kareltje rechts van de stip staan om de plank net niet te laten kantelen?
- Gegevens
- De plank heeft een massa van 15 kg. De zwaartekracht die werkt op de plank is dan Fz = 15 * 9,8 = 147 N.
- De massa van Kareltje is 30 kg. Op Kareltje werkt dus een zwaartekracht van Fz = 30 * 9,8 = 294 N.
- De afstand tussen het zwaartepunt van de plank (waaruit de gehele zwaartekracht van de plank werkt) en het draaipunt (rode stip) bedraagt 0,6 meter.
- Gevraagd: de afstand die Kareltje rechts van het draaipunt op de plank kan gaan staan om het geheel nog net in evenwicht te laten zijn.
- Formule
- Momentenwet: M = F * r, en in evenwichtssituaties geldt er
- M = Fp * rp = Fk * rk=. Oftelwel:
- Moment = Zwaartekracht plank * arm plank = Zwaartekracht Kareltje * arm Kareltje.
- Invullen
- M = Fp * rp = Fk * rk = 147 N * 0,6 m = 294 N * rk = 88,2 Nm
- Dus 88,2 Nm = 294 N * rk, ombouwen geeft rk = 88,2/294 = 0,3 meter.
- Antwoord: Kareltje kan maximaal op een afstand van 0,3 meter rechts van het draaipunt op de plank staan om deze net niet te laten kantelen.
- Gegevens
- De oppervlakte van de kop van de spijker is 0,8 cm² ( = 0,00008 m²).
- De punt van de spijker heeft een oppervlakte van 2 mm². ( = 0,000006 m²).
- Op de kop van de spijker wordt een kracht van 750 N uitgeoefend.
- Gevraagd: kracht die de punt van de spijker uitoefent op het hout wanneer deze er in geslagen wordt.
- Formule
- Druk: p = F/A
- Invullen
- p = F/A = 750 N / 0,00008 m² = 9375000 N/m²
- Deze druk wordt ook door de punt van de spijker vervolgens uitgeoefend, maar het oppervlakte is kleiner.
- De kracht die de punt van de spijker dan uitoefent kan dan uitgerekend worden met F = p * A, dit invullen geeft:
- 9375000 N/m² * 0,000006 m² = 56,25 Newton.
- Antwoord: De punt van de spijker oefent dan een kracht van 56,25 N uit op het hout.
Deze toets bestellen?
Voordeligst
Lidmaatschap ToetsMij
€ 12,99/mnd
- Snel nog even wat toetsen oefenen? Kies dan onze meest flexibele optie.
- Je kunt maandelijks opzeggen.
- Toegang tot alle vakken bij ToetsMij.
Wat krijg je bij een abonnement?
- Toegang tot alle vakken
- 20 kwalitatieve oefentoetsen per maand
- Antwoorden, uitwerkingen en toelichtingen
- Geen stress voor het maken van toetsen
Eenvoudig en veilig betalen met iDEAL of creditcard
3 maanden ToetsMij
€ 12,99
€ 10,99/mnd
- Voordelig en flexibel. Ideaal als je maar een paar maanden toetsen hoeft te gebruiken.
- Betaal per kwartaal en bespaar hiermee 2 euro per maand.
- Toegang tot alle vakken bij ToetsMij.
Wat krijg je bij een abonnement?
- Toegang tot alle vakken
- 20 kwalitatieve oefentoetsen per maand
- Antwoorden, uitwerkingen en toelichtingen
- Geen stress voor het maken van toetsen
Eenvoudig en veilig betalen met iDEAL of creditcard
1 jaar ToetsMij
€ 12,99
€ 7,50/mnd
- Favoriete keuze van meer dan 70% van de gebruikers.
- Betaal slechts 90 euro per jaar en bespaar hiermee 65 euro.
- Geniet van een volledig jaar toegang tot alle vakken bij ToetsMij.
Wat krijg je bij een abonnement?
- Toegang tot alle vakken
- 20 kwalitatieve oefentoetsen per maand
- Antwoorden, uitwerkingen en toelichtingen
- Geen stress voor het maken van toetsen
Eenvoudig en veilig betalen met iDEAL of creditcard
Waarom ToetsMij?
- Betere schoolresultaten
- Geen stress meer omdat je weet wat je moet doen om je toetsen te halen
- Direct toegang tot antwoorden en uitwerkingen zodat je weet wanneer je klaar bent voor je toets
Heb je nog vragen?
Neem eenvoudig contact met ons op, of kijk bij onze veelgestelde vragen.
Dit zeggen leerlingen en ouders
Cijfers omhoog
Onze zoon had in februari zeker 12 minpunten. Hij is gestart met oefenen via Toets mij en heeft een geweldige eindsprint getrokken en afgelopen week bijna het onmogelijke waargemaakt. Er zijn nog maar 2 minpunten over en nog niet alle toetsen zijn terug. Het heeft onze zoon enorm geholpen, omdat er breed getoetst wordt en de vraagstelling, zoals van hem begrepen, overeenkomt met de toets. Als je de oefentoetsen goed kunt maken, beheers je de stof echt goed!
AP
Fijn dat leerlingen alvast een keer een toets kunnen oefenen die eruit ziet zoals op school.
Wij hebben sinds kort Toetsmij, omdat onze dochter het erg lastig heeft met Wiskunde. Op deze manier kan ze het hoofdstuk oefenen met een toets die qua vraagstelling overeenkomt met de toetsen op school. Nu kan ze dit dus eerst oefenen voordat ze de echte toets moet doen. Als docent Engels die werkt met Of Course en All Right kan ik bevestigen dat de toetsen grotendeels overeenkomen met de vraagwijze van de methode zelf. Dat is dus heel fijn voor leerlingen om te oefenen. We hadden heel even een dingetje met het nakijken, want de uitwerkingen werden niet goed weergegeven. Even een mailtje en binnen een dag reactie en ICT ging meteen aan de slag met het herstellen van de uitwerkingen. Super contact, goede dienstverlening! Aanrader!
Lelani van den Berg
Zéér tevreden!!
Lid geworden voor mijn zoon in leerjaar 1 van (toen 13) inmiddels 15. Hij zit nu in leerjaar 3 HAVO. Elk boek is makkelijk te vinden en alsmede mailt met een probleem omdat hij Duits krijgt uit een boek van leerjaar 2 word dit zelfs op zondag binnen een half uur opgelost en toegevoegd aan ons account! Zo’n toffe service zie je niet vaak meer! Dus wij zijn zéér tevreden. Sinds we het nu weer gebruiken (tijdje niet gebruikt) scoort hij weer voldoendes en zelf voor wiskunde een 8.8!
Linda Ockers
Zoek in meer dan 10.000 toetsen
Echte toetsvragen, precies aansluitend op jouw lesmethode en leerjaar. Voor klas 1 t/m 6 van vmbo-t t/m gymnasium.
