Toets Natuurkunde

Nova Natuurkunde 4e ed - Hoofdstuk 5 - Kracht en beweging oefentoetsen & antwoorden

4e editie

Klas 3|Vwo/gymnasium

Deze toets behandelt de volgende onderwerpen: Bewegingen, Bewegingen in diagrammen, Versnelling, Luchtweerstand, Resultante kracht, Eerste wet van Newton, Tweede wet van Newton, Valbewegingen, Krachten ontbinden, Stopafstand, Botsen, Druk, G-krachten.

Nova Natuurkunde 4e ed
Toets Natuurkunde
Nova Natuurkunde 4e ed
Online maken
Toets afdrukken
  • a) Eenparige beweging (snelheid is constant)
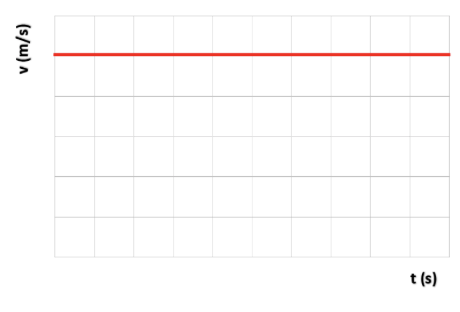
  • Eenparig versnelde beweging (snelheid neemt met constante waarde toe)
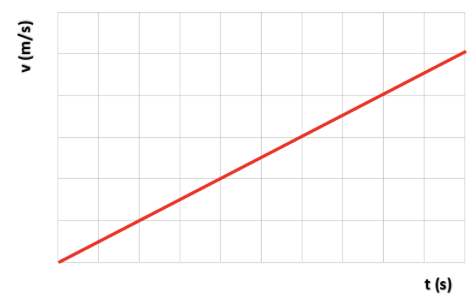
  • Eenparig vertraagde beweging (snelheid neemt met constante waarde af)
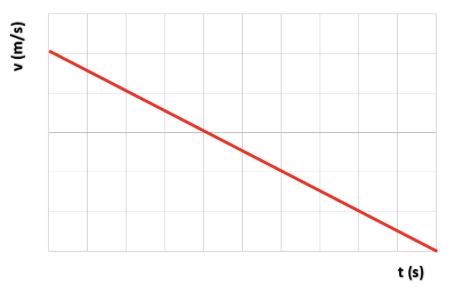
  • b) De straalmotor perst de verbrandingsgassen de motor uit. De motor oefent een kracht uit in de richting van de uitlaat. Dit is de actie. Volgens de Derde Wet van Newton oefenen de uitgestoten gasdeeltjes een even grote tegengestelde kracht uit. Dit noemen we de reactiekracht. 
  • c) Dat zijn:
    • De Cw-waarde
    • Het frontale oppervlak
    • De dichtheid van de lucht
    • De snelheid van het object
  • d) Traagheid geeft aan hoe moeilijk het is om een object in beweging te krijgen. Er geldt hoe groter de massa, hoe meer kracht nodig is om dit in beweging te krijgen. Dus hoe meer massa een object heeft, hoe groter zijn traagheid is.
  • e) Dat betekent dat er dan een versnelling van 1 g op iemand werkt. g is de valversnelling hier op aarde en die is gemiddeld genomen 9,8 m/s². Er werkt dan dus een versnelling van  9,8 m/s² op iemand.
  • f) Doordat de kat een kleinere massa heeft, werkt er minder zwaartekracht op de kat ten opzichte van de mens. Doordat er meer kracht op de mens werkt, is de impact die de mens maakt op de grond groter ten opzichte van een kat.
  • g) De rolwrijving is een constante waarde. Bij het begin van de race moet de racewagen een opstarten en een grotere voorwaartse kracht hebben dan de rolwrijving. Tijdens de race levert de motor van de racewagen in ieder geval al meer kracht dan de rolwrijving, omdat de racewagen dan in ieder geval al snelheid heeft. DIt betekent dat de rolwrijving tijdens de start bij het optrekken een grotere rol speelt.
 
  • a) Gegevens: 
    • Δt = 1 sec.
    • Δv = 2 m/s
  • Gevraagd: a = ?
  • Formule: a = Δv / Δt
  • Invullen: a = Δv / Δt = 2 / 1 = 2 m/s²
  • Antwoord: De versnelling tijdens de eerste seconde is 2 m/s²
  • b) Toelichting; In de onderstaande afbeelding zie je hoe het diagram gebruikt wordt voor de berekening. Het geel gemarkeerde gedeelte ligt onder de grafiek en kan meegenomen worden in de berekening. De oppervlakte onder het diagram dat donkergroen gemarkeerd is, wordt vervangen door het licht groen gemarkeerde gedeelte. De oppervlakte onder het lichtgroene en donkergroene (met de gele horizontale lijn als grens) hebben ongeveer dezelfde oppervlakte. De gemiddelde snelheid wordt hierdoor op ca. 3,2 m/s geschat.

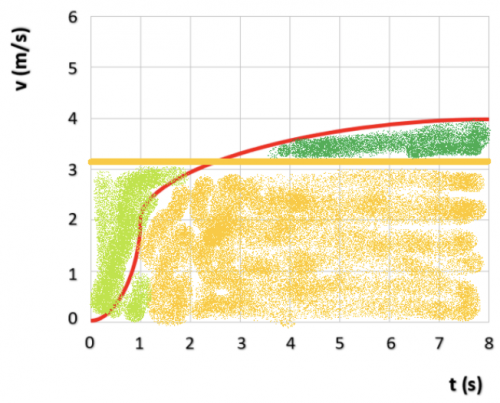
  • Gegevens: 
    • t = 8 sec.
    • v = 3,2 m/s
  • Gevraagd: s = ?
  • Formule: s = vgem *  t
  • Invullen: s = vgem *  t = 3,2 * 8 = 25,6 m 
  • Antwoord: De afgelegde weg na 8 seconden is 25,6 m.
  • c) De resulterende kracht is het kleinst wanneer er een zo klein mogelijk versnelling is. Je moet in het diagram dus kijken naar wanneer de snelheidsverandering zo klein mogelijk is. Dit is tussen t = 7s en t = 8s. De snelheid verandert tussen t = 7s en t = 8s nauwelijks nog. Dit betekent dat daar de kleinste versnelling te zien is en dat betekent dat daarvoor de kleinste resulterende kracht nodig is.
 
  • a) De formule voor luchtwrijving is F = ½ * ρ * Cw * A * v². Het oppervlak van een cirkel kan berekend worden met A = πr². Dus hoe groter de straal van de bol, hoe groter zijn oppervlak. In de formule voor luchtwrijving betekent dit dat hoe groter het oppervlak, hoe groter de luchtwrijving ook zal zijn. Bal B zal dus de grootste luchtwrijving van de twee ballen ondervinden.
  • b) Gegevens: 
    • ρ = 1,293 kg/m³
    • Cw = 0,1
    • rA = 6 cm = 0,06 m
    • rB = 12 cm = 0,12 m
    • AA = π * r² = π * 0,06² = 0,0113097336 m²
    • AB = π * r² = π * 0,12² = 0,0452389342 m²
    • Aandrijvende kracht = 0,05 N
  • Gevraagd: Snelheidsverschil bal A en B.
  • Formule: F = ½ * ρ * Cw * A * v², ombouwen geeft v² = F / (½ * ρ * Cw * A) 
  • Invullen:  
  • Snelheid bal A
    • v² = F / (½ * ρ * Cw * A) = 0,05 / (½ * 1,293 * 0,1 * 0,0113097336) = 68,3831496
    • Wortel trekken geeft: v = √v² = √68,3831496 = 8,26941047 ≈ 8,27 m/s
  • Snelheid bal B
    • v² = F / (½ * ρ * Cw * A) = 0,05 / (½ * 1,293 * 0,1 * 0,0452389342) = 17,0957875
    • Wortel trekken geeft: v = √v² = √17,0957875 = 4,13470525 ≈ 4,13 m/s
    • Verschil: 8,27 - 4,13 = 4,14 m/s
  • Antwoord: De hamster zal in Bal A dus 8,27 - 4,13 = 4,14 m/s sneller zijn dan in bal bal B.
  • c) De straal van Bal B is tweemaal zo groot als die van Bal A. Wanneer we kijken naar de formule voor de inhoud van een bol is dit: 4/3 * π * r³. Dus een 2 maal zo grote straal geeft een volume voor Bal B dat 2³ =  8 maal zo groot is als die van Bal A. In Bal B zullen dus in ieder geval meer zakjes water passen en dus zal de massa van Bal B groter zijn dan die van Bal A wanneer beide gevuld zijn met de zakjes water. 
  • De valversnelling a is constant in de formule F = m * a, omgebouwd: a = F/m. Dus wanneer de massa van een voorwerp bijvoorbeeld driemaal zo groot is, zal de zwaartekracht die hierop zal werken ook driemaal zo groot zijn. De waarde voor a moet immers constant blijven. Dit betekent in deze situatie dat op Bal B de grootste zwaartekracht zal werken, omdat Bal B van de twee ballen de grotere massa heeft.
 
  • De Derde Wet van Newton luidt: Actie = - Reactie. Oftewel tegen de actiekracht werkt een exact tegengestelde reactiekracht. Dus wat gebeurt er? De man oefent een kracht uit op de muur door hier tegenaan te leunen. Dit is de actiekracht. Echter, een muur verplaatst zich niet wanneer je ertegen aanleunt. De muur oefent dus een kracht uit die ervoor zorgt dat de gehele situatie in balans is (dus de resulterende kracht is 0N), want de muur beweegt niet. Dit betekent dat de muur een even grote kracht uitoefent, maar in exact de tegengestelde richting als de actiekracht van de man. Dus er geldt inderdaad: Actie = - Reactie.
  • Opmerking: Wellicht denk je in deze situatie aan de normaalkracht die in hoofdstuk 1 aan bod is gekomen. De normaalkracht is inderdaad de reactiekracht in deze (en vele andere) situaties.
 
  • a) Gegevens: 
    • Ftrek = 55 N
    • α = 40°
  • Gevraagd: Grootte wrijvingskracht
  • Invullen: 
    • Fwrijving = Ftrek * cos α
    • Fwrijving = 55 * cos 40° = 42,1324444 ≈ 42,13 N
  • Antwoord: De wrijvingskracht is 42,13 N.
  • b) Gegevens: 
    • Ftrek = 55 N
    • Fwrijving = 42,13 N
    • a = 0,45 m/s²
    • m = 6,5 kg
  • Gevraagd: Hoek α
  • Formule: F = m * a
  • Invullen:
  • Bereken resulterende kracht
    • F = m * a = 6,5 * 0,45 = 2,925 N
  • Totale kracht
    • F = 42,13 + 2,925 = 45,055 N
  • Hoek berekenen
    • cos-1(α) = cos-1(45,055 / 55) = 34,997 ≈ 35°
 
  • Antwoord: De hoek met het touw zou dan 35° moeten zijn.
 
  • a) Voordat je het v,t-diagram kan tekenen, moet je eerst de snelheid in m/s weten en de remtijd berekend hebben:
  • Gegevens: 
    • vbegin = 90 km/h, in m/s is dit 90/3,6 = 25 m/s
    • veind = 0 m/s
    • Δv = 25 - 0 = 25 m/s
    • a = 8,0 m/s²
  • Gevraagd: Remtijd 
  • Formule: a = Δv / Δt, omgebouwd is dit Δt = Δv / a
  • Invullen: Δt = Δv / a = 25 / 8 = 3,125 s
  • Antwoord: De remtijd bedraagt 3,125 seconden.
  • Alle gegevens die nodig zijn voor het v,t-diagram: beginsnelheid = 25 m/s, eindsnelheid = 0 m/s, reactietijd = 1,5 seconde en remtijd = 3,125 seconden. De stopafstand speelt zich dus af in een tijd van 1,5 + 3,125 = 4,625 seconden. Dit geeft het volgende v,t-diagram:
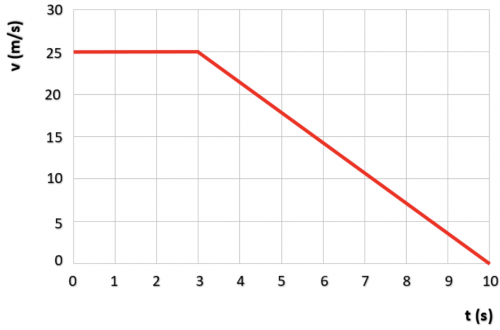
  • b) Formule: 
    • s = v * t
    • s = ½ * v * t (oppervlakteformule driehoek: A = ½ * l * b)
  • Invullen:
  • t = 0s t/m t = 1,5s
    • Het oppervlak onder dit deel van het bovenstaande  v,t-diagram staat gelijk aan de oppervlakte van een rechthoek met als lengte 25 m/s en als breedte 1,5s. Invullen:
    • s = v * t = 25 * 1,5 = 37,5 m
  • t = 1,5s t/m 4,625s
    • Het oppervlak onder dit deel van het diagram staat gelijk aan de oppervlakte van een driehoek met als lengte 25 m/s en als breedte t = 4,625 - 1,5 = 3,125s. Invullen:
    • s = v * t = ½ * 25 * 3,125 = 39,0625 m
  • Totale stopafstand
    • De stopafstand is de som van de berekende afstanden, dus: 37,5 + 39,0625 = 76,5625 m
  • Antwoord: De stopafstand van deze beweging is 76,5625 meter.
 
  • c) Gegevens: 
    • m = 1200 + 1400 = 2600 (de massa van de auto en de caravan)
    • a = 8,0 m/s²
  • Gevraagd: F = ?
  • Formule: F = m * a
  • Invullen: F = m * a = 2600 * 8  = 20800 N = 20,8 kN
  • Antwoord: Hiervoor is een remkracht van 20,8 kN nodig.
 
  • d) Zonder caravan is de massa die geremd van het geheel moet worden kleiner en gaat het maar om één object. Wanneer een caravan aan een auto vastzit, rijdt deze met dezelfde snelheid als de auto. Dit betekent dat wanneer de auto afremt, de caravan in de eerste instantie van achteren tegen de auto aan blijft duwen. De snelheid van de caravan is namelijk op dat moment groter. Omdat de caravan een grote massa heeft, heeft de caravan ook een grotere traagheid. Dat betekent dat er een grote resultante kracht nodig is om de caravan in beweging te laten komen, maar ook dat (wanneer de caravan beweegt) er een grote resultante kracht nodig is om de caravan tot stilstand te laten komen. De auto moet genoeg remkracht leveren om zowel de auto als de caravan tot stilstand te brengen. Wanneer dit in een korte tijd nodig is (omdat er op de weg iets onverwachts gebeurt), is het daardoor in deze situaties met een caravan nog gevaarlijker.
  • De bestuurder ervaart een druk van 20000 Pa tijdens het remmen van zijn gordel (contactoppervlak = 300 cm²). 
  • e) Gegevens: 
    • P = 20000 Pa
    • a = 8 m/s²
    • A = 300 cm² = 0,03 m² 
  • Gevraagd: m = ?
  • Formules: 
    • P = F/A, omgebouwd is dit F = P * A
    • F = m * a, omgebouwd is dit m = F/a
    • Invullen: 
  • Kracht uitrekenen
    • F = P * A = 20000 * 0,03  = 600N
  • Massa berekenen
    • m = F/a invullen geeft: m = F/a = 600N / 8 m/s² = 75 kg.
  • Antwoord: De massa van de bestuurder is 75 kg.
 
  • f) Gegevens: 
    • 1 g = 9,8 m/s²
    • a = 8 m/s²
  • Gevraagd: Groote G-kracht
  • Invullen: 8/9,8 = 0,816326531 ≈ 0,52
  • Antwoord: De G-kracht is 0,52 g.
  • g) Antwoord: Je kan beter dan in de auto zitten.
  • Toelichting: De auto is erop ingericht om bij een botsing de versnelling kleiner te maken door Δv zo klein mogelijk te maken en Δt zo groot mogelijk te maken. De auto heeft veiligheidsgordels, een kreukelzone en airbags. Caravans hebben vaak niet alle of geen van deze veiligheidsvoorzieningen. Je kan dus tijdens een botsing het beste in een auto zitten en niet in een caravan.
  • h) De normaalkracht is even groot als het gewicht dat de auto uitoefent op de weg. Het gewicht staat gelijk aan de zwaartekracht die uitgeoefend wordt op de auto.
  • Gegevens: 
    • g = 9,8 m/s²
    • m = 1200 kg
    • Rolwrijving = 9100 N
  • Gevraagd: Wrijvingscoëfficiënt f
  • Formule: 
    • Fz = m * g
    • f = maximale rolwrijving / normaalkracht
    • Invullen: 
  • Normaalkracht berekenen
    • Fn = m * g = 1200 * 9,8 = 11760 N
  • Wrijvingscoëfficiënt berekenen
    • f = maximale rolwrijving / normaalkracht = 9100 / 11760 = 0.773809524 ≈ 0,774
  • Antwoord: De rolwrijvingscoëfficiënt f is 0,774.
 
  • i) Er zouden spoilers op de auto geplaatst kunnen worden. Door spoilers te gebruiken werkt er een kracht verticaal omlaag en wordt de auto dus meer tegen de weg gedrukt. Daardoor is de kans om te slippen kleiner en heeft de auto dus meer grip op de weg.
  • j) Gegevens: 
    • fnat = 0,774
    • Fn = 11760 N
  • f is 20% kleiner bij regen
  • Gevraagd: Rolwrijving wanneer het droog is
  • Formule: 
    • Fw,max = f * Fn
  • Invullen: 
  • Wrijvingscoëfficiënt berekenen
  • f is bij regen 20% en is dan dus 0,774. Dus wanneer het droog is, heeft f als waarde: (0,774/80) * 100 = 0,9675
  • Maximale rolwrijving berekenen
  • Fw,max = f * Fn invullen geeft: 
    • Fw,max = f * Fn = 11760 * 0,9675 = 11377,8 N.
  • Antwoord: De maximale rolwrijvingskracht bedraagt dan 11377,8 Newton.

Deze toets bestellen?

Voordeligst
Lidmaatschap ToetsMij
€ 12,99/mnd
  • Snel nog even wat toetsen oefenen? Kies dan onze meest flexibele optie.
  • Je kunt maandelijks opzeggen.
  • Toegang tot alle vakken bij ToetsMij.
Kies dit abonnement

Wat krijg je bij een abonnement?

  • Toegang tot alle vakken
  • 20 kwalitatieve oefentoetsen per maand
  • Antwoorden, uitwerkingen en toelichtingen
  • Geen stress voor het maken van toetsen
Eenvoudig en veilig betalen met iDEAL of creditcard
3 maanden ToetsMij
€ 12,99
€ 10,99/mnd
  • Voordelig en flexibel. Ideaal als je maar een paar maanden toetsen hoeft te gebruiken.
  • Betaal per kwartaal en bespaar hiermee 2 euro per maand.
  • Toegang tot alle vakken bij ToetsMij.
Kies dit abonnement

Wat krijg je bij een abonnement?

  • Toegang tot alle vakken
  • 20 kwalitatieve oefentoetsen per maand
  • Antwoorden, uitwerkingen en toelichtingen
  • Geen stress voor het maken van toetsen
Eenvoudig en veilig betalen met iDEAL of creditcard
1 jaar ToetsMij
€ 12,99
€ 7,50/mnd
  • Favoriete keuze van meer dan 70% van de gebruikers.
  • Betaal slechts 90 euro per jaar en bespaar hiermee 65 euro.
  • Geniet van een volledig jaar toegang tot alle vakken bij ToetsMij.
Kies dit abonnement

Wat krijg je bij een abonnement?

  • Toegang tot alle vakken
  • 20 kwalitatieve oefentoetsen per maand
  • Antwoorden, uitwerkingen en toelichtingen
  • Geen stress voor het maken van toetsen
Eenvoudig en veilig betalen met iDEAL of creditcard

Dit zeggen leerlingen en ouders

10

Cijfers omhoog

Onze zoon had in februari zeker 12 minpunten. Hij is gestart met oefenen via Toets mij en heeft een geweldige eindsprint getrokken en afgelopen week bijna het onmogelijke waargemaakt. Er zijn nog maar 2 minpunten over en nog niet alle toetsen zijn terug. Het heeft onze zoon enorm geholpen, omdat er breed getoetst wordt en de vraagstelling, zoals van hem begrepen, overeenkomt met de toets. Als je de oefentoetsen goed kunt maken, beheers je de stof echt goed!

AP
9.0

Fijn dat leerlingen alvast een keer een toets kunnen oefenen die eruit ziet zoals op school.

Wij hebben sinds kort Toetsmij, omdat onze dochter het erg lastig heeft met Wiskunde. Op deze manier kan ze het hoofdstuk oefenen met een toets die qua vraagstelling overeenkomt met de toetsen op school. Nu kan ze dit dus eerst oefenen voordat ze de echte toets moet doen. Als docent Engels die werkt met Of Course en All Right kan ik bevestigen dat de toetsen grotendeels overeenkomen met de vraagwijze van de methode zelf. Dat is dus heel fijn voor leerlingen om te oefenen. We hadden heel even een dingetje met het nakijken, want de uitwerkingen werden niet goed weergegeven. Even een mailtje en binnen een dag reactie en ICT ging meteen aan de slag met het herstellen van de uitwerkingen. Super contact, goede dienstverlening! Aanrader!

Lelani van den Berg
10

Zéér tevreden!!

Lid geworden voor mijn zoon in leerjaar 1 van (toen 13) inmiddels 15. Hij zit nu in leerjaar 3 HAVO. Elk boek is makkelijk te vinden en alsmede mailt met een probleem omdat hij Duits krijgt uit een boek van leerjaar 2 word dit zelfs op zondag binnen een half uur opgelost en toegevoegd aan ons account! Zo’n toffe service zie je niet vaak meer! Dus wij zijn zéér tevreden. Sinds we het nu weer gebruiken (tijdje niet gebruikt) scoort hij weer voldoendes en zelf voor wiskunde een 8.8!

Linda Ockers
Bekijk alle reviews

Zoek in meer dan 10.000 toetsen

Echte toetsvragen, precies aansluitend op jouw lesmethode en leerjaar. Voor klas 1 t/m 6 van vmbo-t t/m gymnasium.

Ik zit in het
en doe
ik wil beter worden in